Largest Rectangular Area in a Histogram

/ DSA / By
Spread the love

In a given histogram, find the greatest rectangular area that can be formed by a number of contiguous bars with heights provided in an array. Assume for the sake of simplicity that the width of each bar is one unit.

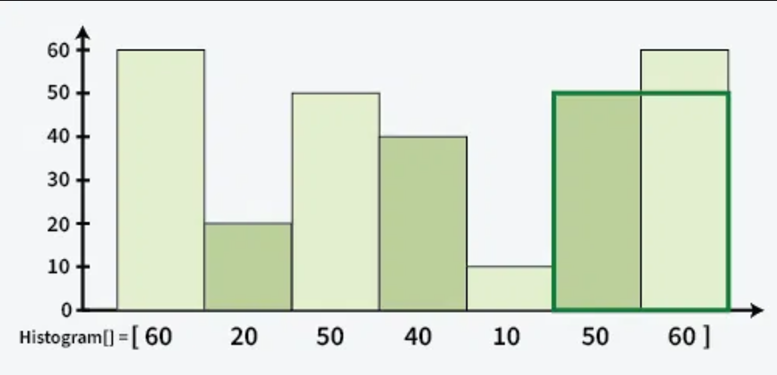
Table of Content

Simple Approach: O(n^2) Time as well as O(1) Space

  • Examine every bar of the histogram and, using it as the minimum height bar, determine the largest area we may have.
  • How can we determine the maximum area with current bar as minimal height? We head left of it and add its height till we come upon a smaller piece. We treat the right side of it similarly. Thus, the minimal area with current bar will equal height of current bar times total width crossed on both left and right, including the current bar.
  • At last we return the maximum of all areas (as determined by considering every bar as minimum height).

C++

#include <bits/stdc++.h>
using namespace std;

int getMaxArea(vector<int> &hist){
    int res = 0, n = hist.size();
  
    // Consider every bar one by one
    for(int i = 0; i < n; i++){
        int curr = hist[i];
      
        // Traverse left while we have a greater height bar
        for(int j = i-1; j>=0 && hist[j] >= hist[i]; j--)
             curr += hist[i];
      
        // Traverse right while we have a greater height bar      
        for(int j = i+1; j<n && hist[j] >= hist[i]; j++)
            curr += hist[i];
      
        res = max(res, curr);
    }
    return res;
}

int main() 
{ 
    vector<int> hist =  {60, 20, 50, 40, 10, 50, 60};
    cout << getMaxArea(hist);
    return 0; 
}

C

#include <stdio.h>

int getMaxArea(int hist[], int n) {
    int res = 0;

    // Consider every bar one by one
    for (int i = 0; i < n; i++) {
        int curr = hist[i];

        // Traverse left while we have a greater height bar
        for (int j = i - 1; j >= 0 && hist[j] >= hist[i]; j--) {
            curr += hist[i];
        }

        // Traverse right while we have a greater height bar
        for (int j = i + 1; j < n && hist[j] >= hist[i]; j++) {
            curr += hist[i];
        }

        if (curr > res) {
            res = curr;
        }
    }

    return res;
}

int main() {
    int hist[] = {60, 20, 50, 40, 10, 50, 60};
    int n = sizeof(hist) / sizeof(hist[0]);
    printf("%d\n", getMaxArea(hist, n));
    return 0;
}

Java

import java.util.*;

class GfG {
    static int getMaxArea(int[] hist) {
        int res = 0, n = hist.length;
        
        for (int i = 0; i < n; i++) {
            int curr = hist[i];
            
            // Traverse left while we have a greater height bar
            for (int j = i - 1; j >= 0 && hist[j] >= hist[i]; j--)
                curr += hist[i];
            
            // Traverse right while we have a greater height bar
            for (int j = i + 1; j < n && hist[j] >= hist[i]; j++)
                curr += hist[i];
            
            res = Math.max(res, curr);
        }
        return res;
    }
    
    public static void main(String[] args) {
        int[] hist = {60, 20, 50, 40, 10, 50, 60};
        System.out.println(getMaxArea(hist));
    }
}

Python

def get_max_area(hist):
    res = 0
    n = len(hist)
    
    for i in range(n):
        curr = hist[i]
        
        # Traverse left while we have a greater height bar
        j = i - 1
        while j >= 0 and hist[j] >= hist[i]:
            curr += hist[i]
            j -= 1
        
        # Traverse right while we have a greater height bar
        j = i + 1
        while j < n and hist[j] >= hist[i]:
            curr += hist[i]
            j += 1
        
        res = max(res, curr)
    
    return res

hist = [60, 20, 50, 40, 10, 50, 60]
print(get_max_area(hist))

C#

using System;

class GfG {
    static int getMaxArea(int[] hist) {
        int n = hist.Length;
        int res = 0;

        // Consider every bar one by one
        for (int i = 0; i < n; i++) {
            int curr = hist[i];

            // Traverse left while we have a greater height bar
            int j = i - 1;
            while (j >= 0 && hist[j] >= hist[i]) {
                curr += hist[i];
                j--;
            }

            // Traverse right while we have a greater height bar
            j = i + 1;
            while (j < n && hist[j] >= hist[i]) {
                curr += hist[i];
                j++;
            }

            res = Math.Max(res, curr);
        }

        return res;
    }

    static void Main(string[] args) {
        int[] hist = {60, 20, 50, 40, 10, 50, 60};
        Console.WriteLine(getMaxArea(hist));
    }
}

JavaScript

function getMaxArea(hist)
{
    let n = hist.length;
    let res = 0;

    // Consider every bar one by one
    for (let i = 0; i < n; i++) {
        let curr = hist[i];

        // Traverse left while we have a greater height bar
        let j = i - 1;
        while (j >= 0 && hist[j] >= hist[i]) {
            curr += hist[i];
            j--;
        }

        // Traverse right while we have a greater height bar
        j = i + 1;
        while (j < n && hist[j] >= hist[i]) {
            curr += hist[i];
            j++;
        }

        res = Math.max(res, curr);
    }

    return res;
}

// Driver code
let hist = [ 60, 20, 50, 40, 10, 50, 60 ];
console.log(getMaxArea(hist));

Output

100